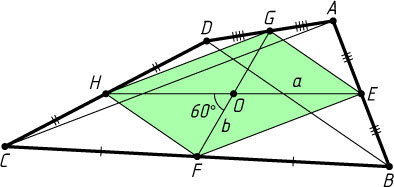
1270. В выпуклом четырёхугольнике ABCD
точки E
, F
, H
, G
являются соответственно серединами отрезков AB
, BC
, CD
, AD
; O
— точка пересечения отрезков EH
и FG
. Известно, что EH=a
, FG=b
, \angle FOH=60^{\circ}
. Найдите диагонали четырёхугольника ABCD
.
Ответ. \sqrt{a^{2}+b^{2}\pm ab}
.
Указание. Четырёхугольник EFHG
— параллелограмм.
Решение. FH
и GE
— средние линии треугольников BDC
и BDA
. Поэтому FH=GE=\frac{1}{2}BD
. EF
и GH
— средние линии треугольников ABC
и ACD
. Поэтому EF=GH=\frac{1}{2}AC
. Следовательно, EFHG
— параллелограмм.
По теореме косинусов находим FH
и GH
из треугольников FOH
и HOG
:
FH^{2}=OF^{2}+OH^{2}-2OF\cdot OH\cos60^{\circ}=\frac{1}{4}(b^{2}+a^{2}-ab),
GH^{2}=OH^{2}+OG^{2}-2OH\cdot OG\cos120^{\circ}=\frac{1}{4}(a^{2}+b^{2}+ab).
Следовательно,
BD=2FH=\sqrt{a^{2}+b^{2}-ab},~AC=2GH=\sqrt{a^{2}+b^{2}+ab}.
Источник: Вступительный экзамен на экономический факультет МГУ. — 1977 (отделение политической экономии), вариант 1. № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 95
