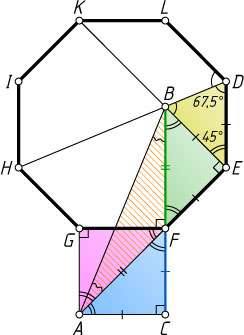
12757. На стороне правильного восьмиугольника DEFGHIKL
во внешнюю сторону построен квадрат ACFG
. В восьмиугольнике проведены диагонали DH
и EK
, пересекающиеся в точке B
. Найдите величину угла ABC
.
Ответ. 22{,}5^{\circ}
Решение. Угол правильного восьмиугольника равен \frac{180^{\circ}(8-2)}{8}=135^{\circ}
. Заметим, что KLDE
— равнобокая трапеция, поэтому
\angle BED=180^{\circ}-135^{\circ}=45^{\circ},~\angle FEB=135^{\circ}-45^{\circ}=90^{\circ}.
Прямая HD
— ось симметрии восьмиугольника, поэтому
\angle HDE=\frac{135^{\circ}}{2}=67{,}5^{\circ}=\angle DBE.
Значит,
EB=ED=EF=FC.
Прямоугольные треугольники BEF
и FCA
равны по двум катетам, поэтому BF=FA
. Треугольник BEF
прямоугольный и равнобедренный, поэтому \angle BFE=45^{\circ}
. Значит,
\angle GFB=\angle GFE-\angle BFE=135^{\circ}-45^{\circ}=90^{\circ}.
При этом \angle CFG=90^{\circ}
, так как ACFG
— квадрат, поэтому точка B
лежит на прямой CF
. Тогда
\angle AFB=\angle AFG+\angle GFB=45^{\circ}+90^{\circ}=135^{\circ}.
Из равнобедренного треугольника AFB
находим, что
\angle FBA+\angle FAB=45^{\circ}.
Следовательно,
\angle ABC=\angle FBA=\frac{45^{\circ}}{2}=22{,}5^{\circ}.
Автор: Кноп К. А.
Источник: Московская математическая олимпиада. — 2022, LXXXV, 8 класс, задача 3
