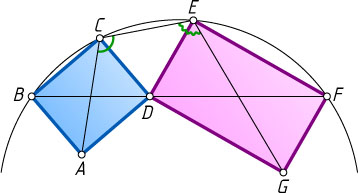
12758. Прямоугольники ABCD
и DEFG
расположены так, что точка D
лежит на отрезке BF
, а точки B
, C
, E
, F
лежат на одной окружности (см. рисунок). Докажите, что \angle ACE=\angle CEG
.
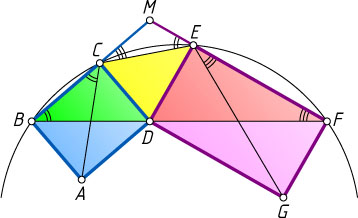
Решение. Пусть прямые BC
и FE
пересекаются в точке M
. Поскольку точки B
, C
, E
, F
лежат на одной окружности, четырёхугольник BCEF
вписанный. Значит,
\angle ECM=\angle DFE,~\angle CEM=\angle DBC.
Поскольку DEFG
и ABCD
— прямоугольники, то
\angle DFE=\angle FEG,~\angle ACB=\angle CBD.
Следовательно,
\angle ACE=180^{\circ}-\angle ECM-\angle ACB=180^{\circ}-\angle FEG-\angle CEM=\angle CEG.
Что и требовалось доказать.
Автор: Бакаев Е. В.
Источник: Московская математическая олимпиада. — 2022, LXXXV, 9 класс, задача 2

