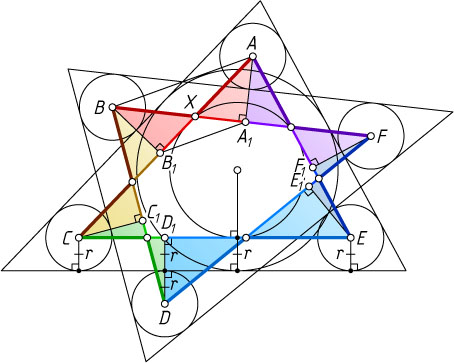
12759. Два треугольника пересекаются по шестиугольнику, который отсекает от них шесть маленьких треугольников. Радиусы вписанных окружностей этих шести треугольников равны. Докажите, что радиусы вписанных окружностей двух исходных треугольников тоже равны.
Решение. Обозначим радиусы шести равных окружностей через r
, а их центры — через A
, B
, C
, D
, E
, F
в порядке обхода против часовой стрелки. Рассмотрим треугольник ACE
. Заметим, что если рассмотреть окружность, вписанную в исходный треугольник, содержащий треугольник ACE
, а затем уменьшить её радиус на r
, оставив центр тем же, то получится окружность, вписанная в треугольник ACE
. Аналогично радиус окружности, вписанной в треугольник BDF
, на r
меньше, чем радиус окружности, вписанной в исходный треугольник, содержащий BDF
. Таким образом, утверждение задачи равносильно равенству радиусов окружностей, вписанных в треугольники ACE
и BDF
.
Опустим перпендикуляры из точки A
на BF
, из B
на AC
и т. д. Обозначим их основания через A_{1}
, B_{1}
и т. д., а точку пересечения AB_{1}
и A_{1}B
— через X
. Тогда отрезки AA_{1}
, BB_{1}
и т. д. равны 2r
. Рассмотрим четырёхугольник AA_{1}B_{1}B
. Он вписанный, поскольку \angle AA_{1}B=\angle AB_{1}B=90^{\circ}
, а так как AA_{1}=BB_{1}
, то AA_{1}B_{1}B
— равнобокая трапеция с основаниями AB
и A_{1}B_{1}
. Следовательно, прямоугольные треугольники AXA_{1}
и BXB_{1}
равны по катету и противолежащему острому углу. Рассматривая трапеции BB_{1}C_{1}C
, CC_{1}D_{1}D
и т. д., получаем аналогичные равенства треугольников и отрезков.
Периметры треугольников ACE
и BDF
равны:
P_{\triangle ACE}=AB_{1}+B_{1}C+CD_{1}+D_{1}E+EF_{1}+F_{1}A=
=A_{1}B+B_{1}C+C_{1}D+DE_{1}+E_{1}F+FA_{1}=P_{\triangle BDF}.
Также равны площади треугольников ACE
и BDF
, поскольку при вырезании из них общего шестиугольника остаётся по шесть прямоугольных треугольников, разбивающихся на пары равных.
Поскольку площадь треугольника равна произведению радиуса вписанной окружности на полупериметр, то из равенства площадей и равенства периметров двух треугольников следует равенство радиусов вписанных в них окружностей.
Автор: Кушнир А. Ю.
Источник: Московская математическая олимпиада. — 2022, LXXXV, 9 класс, задача 5
Источник: Турнир городов. — 2021-2022, XLIII, весенний тур сложный вариант, задача 5, 8-9 классы
