12763. На стороне BC
остроугольного треугольника ABC
отмечены точки D
и E
, причём BD=CE
. На дуге DE
описанной окружности треугольника ADE
, не содержащей точку A
, нашлись такие точки P
и Q
, что AB=PC
и AC=BQ
. Докажите, что AP=AQ
.
Решение. Первый способ. Без ограничения общности будем считать, что точка D
лежит на отрезке BE
и AD\leqslant AE
. Пусть O
— центр описанной окружности \Omega
треугольника ADE
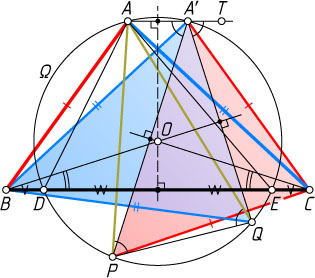
. Пусть точка A'
симметрична A
относительно серединного перпендикуляра к отрезку DE
(рис. 1). Из симметрии A'B=AC=BQ
. Окружность с центром B
и радиусом BA'
пересекает окружность \Omega
в точках, симметричных относительно прямой BO
, т. е. точки A'
и Q
симметричны относительно прямой BO
(обе окружности симметричны относительно их линии центров, значит, точки их пересечения симметричны относительно линии центров). Аналогично, точки A'
и P
симметричны относительно прямой CO
.
Прямые OB
и OC
симметричны относительно серединного перпендикуляра к отрезку DE
, поэтому они образуют равные углы с прямой DE
. Поскольку A'P\perp CO
, A'Q\perp BO
и AA'\parallel DE
, то прямые A'Q
и A'P
образуют равные углы с прямой AA'
.
Пусть T
— точка на продолжении отрезка AA'
за точку A'
. Четырёхугольник APQA'
вписанный, поэтому
\angle AA'P=\angle QA'T=\angle APQ,
Значит, равные вписанные углы AA'P
и APQ
опираются на равные меньшие дуги окружности \Omega
, стягиваемые хордами AP
и AQ
. Следовательно, AP=AQ
. Что и требовалось.
Второй способ. Без ограничения общности будем считать, что точка D
лежит на отрезке BE
. Пусть O
— центр окружности \Omega
, описанной около треугольника ADE
. Заметим, что OB=OC
. Поскольку
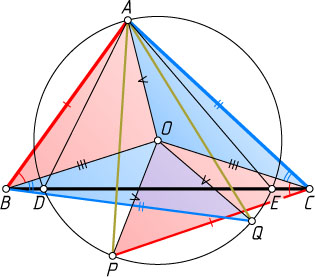
\angle DAE\lt\angle BAC\lt90^{\circ},
точки A
и O
лежат по одну сторону от прямой BC
(рис. 2). Треугольники OAB
и OPC
равны по трём сторонам, треугольники OAC
и OQB
— тоже. Тогда
\angle ABQ=\angle ABO+\angle OBQ=\angle PCO+\angle OCA=\angle PCA.
(Если луч BO
не проходит между сторонами угла ABQ
, то луч BA
проходит между сторонами угла QBO
, а значит, и внутри угла OBC
. В этом случае либо
\angle BOA\gt\angle BOE=\angle COD\gt\angle COP,
либо
\angle BOA\lt\angle BOD=\angle COE\lt\angle COP;
в обоих случаях получаем противоречие с равенством треугольников OAB
и OPC
. Аналогично, луч CO
проходит между сторонами угла PCA
.) Следовательно, треугольники ABQ
и PCA
равны по двум сторонам и углу между ними, откуда AP=AQ
.
Автор: Кузнецов А. С.
Источник: Всероссийская олимпиада школьников. — 2021-2022, XLVIII, заключительный тур, задача 2, 10 класс

