12791. Найдите геометрическое место центров правильных треугольников, вершины которых лежат на сторонах данного квадрата со стороной 1.
Ответ. Образ контура данного квадрата при гомотетии, центром которой является центр данного квадрата, а коэффициент равен \frac{2\sqrt{3}}{3}-1
.
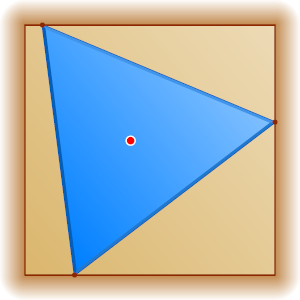
Решение. Пусть правильный треугольник KML
вписан в квадрат ABCD
так, как показано на рисунке 1, а точка P
— середина отрезка KL
. Поскольку
\angle KPM=\angle KBM=90^{\circ},
вокруг четырёхугольника KBMP
можно описать окружность. Следовательно,
\angle MBP=\angle MKP=60^{\circ}.
Аналогично, четырёхугольник LCMP
тоже вписанный, поэтому \angle MCP=60^{\circ}
. Значит, треугольник BPC
тоже правильный. Таким образом, если точки K
, M
и L
двигаются по сторонам AB
, BC
и CD
соответственно, то точка P
остаётся фиксированной (как вершина равностороннего треугольника PBC
). Значит, фиксировано и её расстояние до прямой BC
, равное высоте равностороннего треугольника со стороной 1, т. е. \frac{\sqrt{3}}{2}
. Тогда фиксировано и расстояние от центров O
соответствующих треугольников до BC
, равное \frac{2}{3}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}
. Следовательно, эти центры принадлежат отрезку O_{1}O_{2}
, параллельному BC
.
Концы этого отрезка соответствуют крайним положениям треугольника KML
: O_{1}
— случаю, когда точка K
совпадает с вершиной A
, а O_{2}
— случаю, когда точка L
совпадает с вершиной D
(рис. 2). При этом, если точка K
совпадает с A
, то, в силу симметрии, точка O_{1}
лежит на диагонали AC
. Аналогично, если L
совпадает с D
, то O_{2}
лежит на BD
. Следовательно, если вершины K
, M
и L
перемещаются по указанным сторонам данного квадрата, то центр O
треугольника KML
движется по отрезку O_{1}O_{2}
с концами на диагоналях AC
и BD
. При этом, в силу непрерывности, все промежуточные положения точки на этом отрезке достигаются.
Поскольку вершины треугольника KML
могут располагаться на любых трёх сторонах данного квадрата, то искомое ГМТ состоит из четырёх таких отрезков, которые образуют квадрат с вершинами, расположенными на диагоналях данного квадрата. Его сторона равна разности между ранее найденным расстоянием между прямыми O_{1}O_{2}
, BC
и половиной стороны данного квадрата, т. е. \frac{\sqrt{3}}{3}-\frac{1}{2}
. Значит, искомое ГМТ — квадрат, гомотетичный данному с центром гомотетии, совпадающим с центром данного, и коэффициентом
\frac{\frac{\sqrt{3}}{3}-\frac{1}{2}}{\frac{1}{2}}=\frac{2\sqrt{3}}{3}-1.
Источник: Московская математическая регата. — 2019-2020, четвёртый тур, № 2, 11 класс
