12815. Через произвольную точку K
диаметра AB
окружности проведена хорда CD
, которая образует с AB
угол 45^{\circ}
. Докажите, что величина KC^{2}+KD^{2}
не зависит от выбора точки K
.
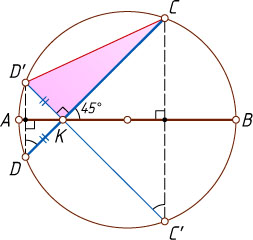
Решение. Первый способ. Пусть точки C'
и D'
симметричны точкам соответственно C
и D
относительно прямой AB
. Поскольку окружность симметрична относительно любого своего диаметра, точки C'
и D'
лежат на окружности, а точка K
лежит на отрезке C'D'
. При этом KD=KD'
и
\angle CKD'=180^{\circ}-\angle CKB-\angle AKD'=180^{\circ}-\angle CKB-\angle AKD=
=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ},~\angle CDD'=45^{\circ}.
Пусть радиус окружности равен R
. По теореме синусов
CD'=2R\sin\angle CDD'=2R\sin45^{\circ}=R\sqrt{2}.
Следовательно,
KC^{2}+KD^{2}=CD'^{2}=2R^{2}.
Отсюда следует утверждение задачи.
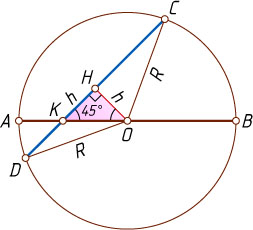
Второй способ. Пусть радиус окружности равен R
, а OH=h
— перпендикуляр, опущенный из центра окружности на хорду CD
. Тогда треугольник OKH
прямоугольный и равнобедренный, поэтому HK=OH=h
.
Без ограничения общности будем считать, что точка H
лежит на отрезке CK
. Поскольку
HC^{2}=HD^{2}=R^{2}-h^{2},
то
KC^{2}+KD^{2}=(HC+HK)^{2}+(HD-HK)^{2}=
=2HC^{2}+2HK^{2}=2(R^{2}-h^{2})+2h^{2}=2R^{2}.
Значит, найденная величина зависит только от радиуса окружности.
Источник: Московская математическая регата. — 2017-2018, пятый тур, № 2, 11 класс

