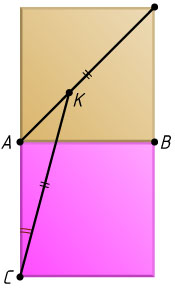
12824. Два квадрата на рисунке имеют общую сторону AB
. На диагонали одного из них отметили точку K
, расстояние от которой до вершины C
другого квадрата равно его диагонали. Найдите угол ACK
.
Ответ. 15^{\circ}
.
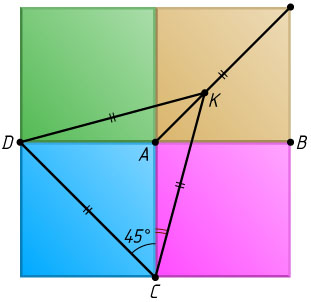
Решение. Первый способ. Построим ещё два квадрата с общей стороной AD
так, как показано на рис. 1, и проведём отрезки CD
и DK
. Тогда полученная картинка симметрична относительно прямой AK
, поэтому CK=DK
. Кроме того, расстояние между C
и K
равно диагонали квадрата, значит, треугольник CDK
— равносторонний, поэтому каждый его угол равен 60^{\circ}
.
Треугольник ADC
равнобедренный и прямоугольный, поэтому \angle ACD=45^{\circ}
. Следовательно,
\angle ACK=60^{\circ}-45^{\circ}=15^{\circ}.
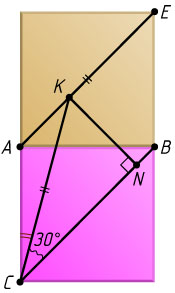
Второй способ. Проведём диагональ BC
нижнего квадрата, которая параллельна диагонали AE
верхнего (рис. 2). Заметим, что расстояние между прямыми AE
и BC
равно половине диагонали квадрата, т. е. равно \frac{1}{2}CK
. Тогда перпендикуляр KN
к прямой BC
также равен \frac{1}{2}CK
. В прямоугольном треугольнике KCN
катет KN
равен половине гипотенузы CK
, значит, \angle KCN=30^{\circ}
. Следовательно,
\angle ACK=\angle ACN-\angle KCN=45^{\circ}-30^{\circ}=15^{\circ}.
Источник: Московская математическая регата. — 2018-2019, третий тур, № 2, 7 класс


