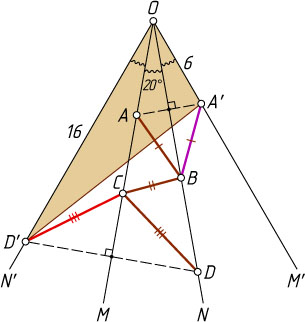
12907. Дан угол MON
, равный 20^{\circ}
. На стороне OM
отмечены точки A
и C
, а на стороне ON
— точки B
и D
. Известно, что OA=6
и OD=16
. Найдите наименьшее значение суммы AB+BC+CD
.
Ответ. 14.
Решение. Пусть A'
— точка, симметричная точке A
относительно прямой ON
, а D'
— точка, симметричная точке D
относительно прямой OM
. Тогда AB=A'B
и CD=CD'
, поэтому
AB+BC+CD=A'B+BC+CD'\geqslant A'D',
причём равенство достигается в случае, когда точки A'
, B
, C
и D'
лежат на одной прямой. Тогда сумма AB+BC+CD
равна стороне A'D'
треугольника A'OD'
, в котором
OA'=OA=6,~OD'=OD=16,~\angle A'OD'=3\cdot20^{\circ}=60^{\circ}.
По теореме косинусов находим, что
A'D'=\sqrt{6^{2}+16^{2}-2\cdot6\cdot16\cdot\cos60^{\circ}}=2\sqrt{9+64-24}=2\cdot7=14.
Источник: Журнал «Crux Mathematicorum». — 2022, № 5, задача OC560, с. 271
Источник: Математические олимпиады ЮАР. — 2019
