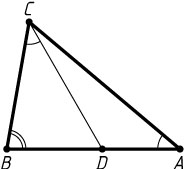
1292. Точка D
лежит на стороне AB
треугольника ABC
, причём \angle BCD=\angle BAC
. Найдите CD
, если AB=c
, BC=a
, AC=b
.
Ответ. \frac{ab}{c}
.
Указание. Треугольник CBD
подобен треугольнику ABC
.
Решение. Треугольник CBD
подобен треугольнику ABC
по двум углам (угол при вершине B
— общий). Значит, \frac{CD}{AC}=\frac{BC}{AB}
. Следовательно,
CD=\frac{AC\cdot BC}{AB}=\frac{ab}{c}.
