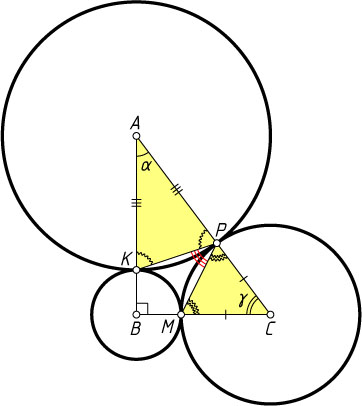
1302. Центры трёх попарно касающихся друг друга внешним образом окружностей расположены в точках A
, B
, C
, \angle ABC=90^{\circ}
. Точки касания — K
, P
и M
; точка P
лежит на стороне AC
. Найдите угол KPM
.
Ответ. 45^{\circ}
.
Указание. Выразите искомый угол через острые углы треугольника ABC
.
Решение. Обозначим
\angle BAC=\alpha,~\angle ACB=\gamma~(\alpha+\gamma=90^{\circ}).
Пусть точка K
лежит на отрезке AB
. Из равнобедренных треугольников KAP
и MCP
находим, что
\angle APK=90^{\circ}-\frac{\alpha}{2},~\angle MPC=90^{\circ}-\frac{\gamma}{2}.
Тогда
\angle KPM=180^{\circ}-(\angle APK+\angle MPC)=180^{\circ}-\left(90^{\circ}-\frac{\alpha}{2}+90^{\circ}-\frac{\gamma}{2}\right)=
=\frac{\alpha+\gamma}{2}=45^{\circ}.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 5.1.25, с. 15
