13039. На сторонах квадрата ABCD
взяты точки M
, N
и K
, где M
— середина стороны AB
, N
лежит на стороне BC
, причём 2BN=NC
, K
лежит на стороне AD
, причём 2DK=KA
. Найдите синус угла между прямыми MC
и NK
.
Ответ. \frac{7\sqrt{2}}{10}
.
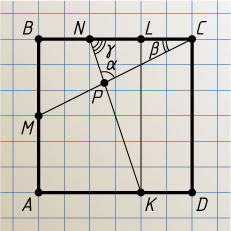
Решение. Пусть L
— середина отрезка CN
, прямые MC
и NK
пересекаются в точке P
, а сторона квадрата равна 6a
. Обозначим \angle CPN=\alpha
, \angle BCM=\beta
, \angle LNK=\gamma
.
Поскольку \frac{CL}{LB}=\frac{DK}{KA}
, прямые KL
и AB
параллельны, поэтому KL\perp BC
. Из прямоугольных треугольников BCM
и LKN
получаем
\tg\beta=\frac{BM}{BC}=\frac{3a}{6a}=\frac{1}{2},~\tg\gamma=\frac{6a}{2a}=3.
Тогда
\tg\alpha=\tg\angle CPN=\tg(180^{\circ}-\beta-\gamma)=-\tg(\beta+\gamma)=
=\frac{\tg\beta+\tg\gamma}{\tg\beta\tg\gamma-1}=\frac{\frac{1}{2}+3}{\frac{1}{2}\cdot3-1}=7,~\ctg\alpha=\frac{1}{7}.
Следовательно,
\sin\alpha=\frac{1}{\sqrt{1+\ctg^{2}\alpha}}=\frac{1}{\sqrt{1+\frac{1}{49}}}=\frac{7}{5\sqrt{2}}=\frac{7\sqrt{2}}{10}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 93, с. 14
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 93, с. 13
