1306. Биссектриса угла, смежного с углом C
треугольника ABC
, пересекает продолжение стороны AB
за точку B
в точке D
, а биссектриса угла, смежного с углом A
, пересекает продолжение BC
за точку C
в точке E
. Известно, что DC=CA=AE
. Найдите углы треугольника ABC
.
Ответ. 12^{\circ}
, 36^{\circ}
, 132^{\circ}
.
Указание. Обозначьте \angle BAC=\alpha
и составьте уравнение относительно \alpha
.
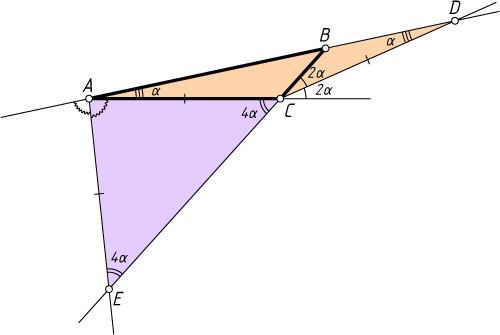
Решение. Пусть \angle BAC=\angle ADC=\alpha
. Внешний угол равнобедренного треугольника ACD
при вершине C
равен 2\alpha
. Тогда внешний угол треугольника ABC
при вершине C
равен 4\alpha
. Значит, \angle CAE=180^{\circ}-8\alpha
. Внешний угол треугольника ABC
при вершине A
вдвое больше угла CAE
, поэтому
\angle BAC=180^{\circ}-2(180^{\circ}-8\alpha)=16\alpha-180^{\circ}.
Из уравнения 16\alpha-180^{\circ}=\alpha
находим, что \alpha=12^{\circ}
. Тогда
\angle ACB=180^{\circ}-4\alpha=180^{\circ}-48^{\circ}=132^{\circ},
\angle ABC=180^{\circ}-(12^{\circ}+132^{\circ})=36^{\circ}.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 5.1.30, с. 15
