1312. Стороны пятиугольника в порядке обхода равны 5, 6, 7, 8 и 9. Стороны этого пятиугольника касаются одной окружности. На какие отрезки точка касания со стороной, равной 5, делит эту сторону?
Ответ. \frac{3}{2}
и \frac{7}{2}
.
Указание. Обозначьте через x
один из искомых отрезков и выразите последовательно через x
отрезки, на которые точки касания делят стороны пятиугольника.
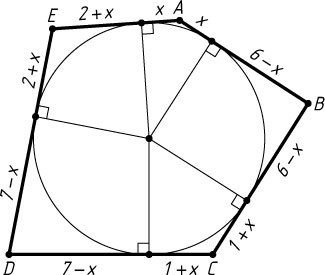
Решение. Обозначим касательные, выходящие из вершины A
, через x
. «Обойдём» наш пятиугольник, выражая последовательно длины касательных из вершин B
(равны 6-x
), C
(равны 7-(6-x)=1+x
), D
(равны 8-(1+x)=7-x
) и E
(равны 9-(7-x)=2+x
). Получим, что сторона AE
точкой касания делится на отрезки x
и 2+x
. Из уравнения x+(2+x)=5
найдём, что x=\frac{3}{2}
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 5.4.9, с. 41
