1318. На сторонах AD
и DC
ромба ABCD
построены правильные треугольники AKD
и DMC
, причём точка K
лежит по ту же сторону от AD
, что и прямая BC
, а точка M
— по другую сторону от DC
, чем AB
. Докажите, что точки B
, K
и M
лежат на одной прямой.
Указание. Докажите, что \angle MBD=\angle KBD
.
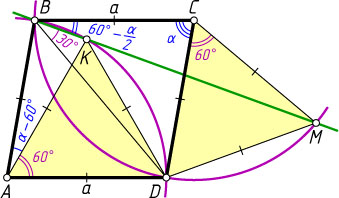
Решение. Первый способ. Пусть угол A
ромба равен \alpha
. Рассмотрим случай, когда 60^{\circ}\leqslant\alpha\leqslant120^{\circ}
. Тогда
\angle BAK=\alpha-60^{\circ},~\angle KBA=90^{\circ}-\frac{\alpha-60^{\circ}}{2}=120^{\circ}-\frac{\alpha}{2},
\angle CBK=\angle ABC-\angle KBA=(180^{\circ}-\alpha)-\left(120^{\circ}-\frac{\alpha}{2}\right)=60^{\circ}-\frac{\alpha}{2}.
С другой стороны,
\angle BCM=\alpha+60^{\circ},~\angle CBM=90^{\circ}-\frac{\alpha+60^{\circ}}{2}=60^{\circ}-\frac{\alpha}{2}.
Из равенства углов CBK
и CBM
заключаем, что точки B
, K
и M
лежат на одной прямой.
Аналогично для остальных случаев.
Второй способ. Пусть a
— сторона ромба. Тогда точки B
, K
и D
лежат на окружности с центром A
и радиусом a
, а точки B
, D
и M
— на окружности того же радиуса с центром в точке C
. Значит, угол MBD
равен половине меньшей дуги MD
второй окружности, т. е. \frac{60^{\circ}}{2}=30^{\circ}
.
С другой стороны, угол KBD
равен половине меньшей дуги KD
первой окружности, т. е. \frac{60^{\circ}}{2}=30^{\circ}
. Из равенства углов MBD
и KBD
следует, что точки B
, K
и M
лежат на одной прямой.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 6.1.13, с. 52
