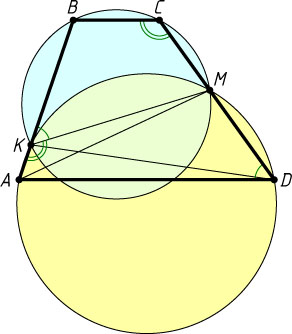
1319. Через концы основания AD
трапеции ABCD
проведена окружность, пересекающая прямые AB
и CD
в точках K
и M
. Докажите, что точки B
, C
, K
и M
лежат на одной окружности.
Указание. Докажите, что либо \angle BKM+\angle BCM=180^{\circ}
, либо \angle BKM=\angle BCM
.
Решение. Рассмотрим случай, когда данная окружность пересекает отрезки AB
и CD
(для остальных случаев аналогично).
\angle BKM=180^{\circ}-\angle AKM=\angle ADM=\angle ADC,
но \angle ADC+\angle BCM=180^{\circ}
, поэтому
\angle BKM+\angle BCM=180^{\circ}.
Следовательно, точки B
, C
, K
и M
лежат на одной окружности.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 6.2.17, с. 61
