1320. Диагонали трапеции с основаниями AD
и BC
пересекаются в точке O
. Докажите, что окружности, описанные около треугольников AOD
и BOC
, касаются друг друга.
Указание. Применив теорему, обратную теореме об угле между касательной и хордой, докажите, что касательная к одной из окружностей, проходящая через точку O
, является также касательной к другой окружности.
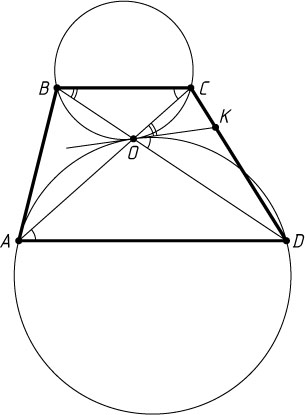
Решение. Первый способ. Рассмотрим луч OK
, пересекающий CD
, и такой, что \angle KOD=\angle OAD
. Докажем, что прямая OK
касается описанной окружности треугольника AOD
. Действительно, если это не так, то через точку O
проведём касательную к этой окружности и возьмём на ней точку Q
по одну сторону с точкой K
от прямой BD
. Тогда
\angle QOD=\angle OAD=\angle KOD.
Следовательно, прямая OK
совпадает с касательной к окружности.
Докажем теперь, что прямая OK
является также касательной к описанной окружности треугольника BOC
. Действительно,
\angle COK=\angle COD-\angle KOD=\angle BOA-\angle OAD=\angle BOA-\angle BCO=\angle CBO
(угол BOA
— внешний угол треугольника BOC
). Из рассуждений, аналогичных приведённым выше, следует, что прямая OK
касается описанной окружности треугольника BOC
.
Второй способ. При гомотетии с центром O
и коэффициентом -\frac{AD}{BC}
треугольник BOC
переходит в треугольник DOA
, описанная окружность треугольника BOC
— в описанную окружность треугольника DOA
, а так как центр гомотетии O
— общая точка этих окружностей, то O
— точка их касания.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 6.2.26, с. 62
