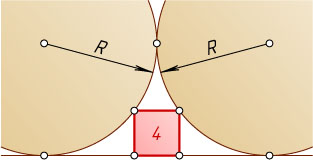
13218. Квадрат площади 4 вписан в криволинейный треугольник, ограниченный дугами двух равных касающихся окружностей радиуса R
и их общей касательной (см.рис.). Найдите R
.
Ответ. 5.
Решение. Пусть прямая касается окружностей с центрами O_{1}
и O_{2}
в точках A
и B
соответственно, вершины M
и N
квадрата KLNM
лежат на первой и второй окружностях соответственно, вершины K
и L
— на прямой AB
, P
— точка пересечения с отрезком AB
общей касательной окружностей, проведённой в точке Q
их касания (P
— середина AB
).
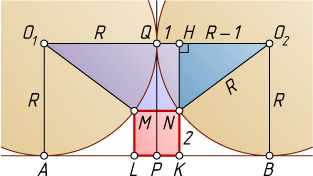
Первый способ. В равнобедренной трапеции O_{1}O_{2}NM
боковые стороны O_{1}M
и O_{2}N
равны R
, основания O_{1}O_{2}
и MN
равны 2R
и 2 соответственно. Проведём высоту NH
трапеции. Тогда
NH=KH-KN=O_{1}A-KN=R-2,~O_{2}H=\frac{O_{1}O_{2}-MN}{2}=\frac{2R-2}{2}=R-1.
Из прямоугольного треугольника O_{2}HN
получаем
O_{2}N^{2}=NH^{2}+O_{2}H^{2},~\mbox{или}~R^{2}=(R-2)^{2}+(R-1)^{2}~\Leftrightarrow~R^{2}-6R+5=0.
Корень R=1
этого уравнения не удовлетворяет условию задачи, так как тогда радиус окружности меньше стороны квадрата. Следовательно, R=5
.
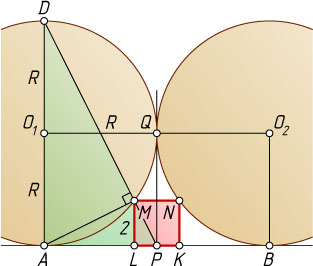
Второй способ. Пусть AD
— диаметр первой окружности. Поскольку \frac{AD}{AP}=2=\frac{ML}{LP}
, точка M
лежит на отрезке DP
, а так как AM
— высота прямоугольного треугольника DAP
, проведённая из вершины прямого угла, то
PM=\frac{AP^{2}}{DP}=\frac{O_{1}Q^{2}}{\sqrt{AP^{2}+AD^{2}}}=\frac{O_{1}Q^{2}}{\sqrt{R^{2}+4R^{2}}}=\frac{R^{2}}{R\sqrt{5}}=\frac{R}{\sqrt{5}}.
С другой стороны,
PM=\sqrt{PL^{2}+ML^{2}}=\sqrt{1+4}=\sqrt{5}.
Из равенства \frac{R}{\sqrt{5}}=\sqrt{5}
находим, что R=5
.
Источник: Олимпиада «Высшая проба» (математическая олимпиада ВШЭ). — 2020, первый этап, задача 4, 11 класс


