13235. Окружность вписана в шестиугольник ABCDEF
. Найдите AF
, если AB=10
, BC=7
, CD=11
, DE=12
, EF=4
.
Ответ. 6.
Решение. Пусть окружность, вписанная в данный шестиугольник, касается его сторон AB
, BC
, CD
, DE
и EF
в точках A_{1}
, B_{1}
, C_{1}
, D_{1}
, E_{1}
и F_{1}
соответственно. Обозначим AF_{1}=t
. Тогда
AA_{1}=AF_{1}=t,~BB_{1}=BA_{1}=AB-AA_{1}=10-t,
CC_{1}=CB_{1}=BC-BB_{1}=7-(10-t)=t-3,
DD_{1}=DC_{1}=CD-CC_{1}=11-(t-3)=14-t,
EE_{1}=ED_{1}=DE-DD_{1}=12-(14-t)=t-2,
FF_{1}=FE_{1}=EF-EE_{1}=4-(t-2)=6-t.
Следовательно,
AF=AF_{1}+FF_{1}=t+(6-t)=6.
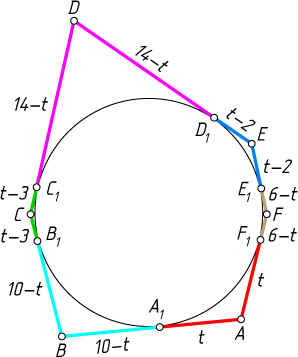
Источник: Олимпиада «Высшая проба» (математическая олимпиада ВШЭ). — 2015, предварительный этап, задача 4, 9 класс
