1324. Высота прямоугольного треугольника, опущенная на гипотенузу, разбивает этот треугольник на два треугольника. Расстояние между центрами вписанных окружностей этих треугольников равно 1. Найдите радиус вписанной окружности исходного треугольника.
Ответ. \frac{1}{\sqrt{2}}
.
Указание. Докажите, что сумма квадратов радиусов двух меньших окружностей равна квадрату радиуса третьей.
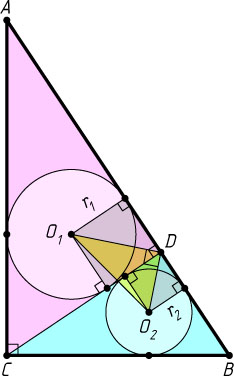
Решение. Пусть ABC
— исходный треугольник, CD
— его высота, опущенная на гипотенузу, O_{1}
и O_{2}
— центры вписанных окружностей треугольников ADC
и CDB
соответственно, r_{1}
и r_{2}
— их радиусы, r
— радиус вписанной окружности треугольника ABC
.
Докажем сначала, что r^{2}=r^{2}_{1}+r^{2}_{2}
. Действительно, треугольник ACB
подобен треугольнику ADC
с коэффициентом \frac{AB}{AC}
, а треугольнику CDB
— с коэффициентом \frac{AB}{BC}
, поэтому
r_{1}=r\cdot\frac{AC}{AB},~r_{2}=r\cdot\frac{BC}{AB}.
Следовательно,
r^{2}_{1}+r^{2}_{2}=\left(r\cdot\frac{AC}{AB}\right)^{2}+\left(r\cdot\frac{BC}{AB}\right)^{2}=\frac{r^{2}(AC^{2}+BC^{2})}{AB^{2}}=r^{2}.
В прямоугольном треугольнике O_{1}DO_{2}
катеты DO_{1}
и DO_{2}
равны соответственно r_{1}\sqrt{2}
и r_{2}\sqrt{2}
, поэтому
1=O_{1}O^{2}_{2}=DO^{2}_{1}+DO^{2}_{2}=\left(r_{1}\sqrt{2}\right)^{2}+\left(r_{2}\sqrt{2}\right)^{2}=2r^{2}_{1}+2r^{2}_{2}=2r^{2}.
Следовательно, r=\frac{1}{\sqrt{2}}
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 7.1.24, с. 84
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — № 27, с. 179
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 46(7), с. 35
