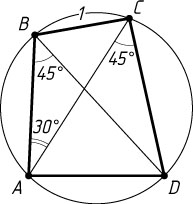
1326. В четырёхугольнике ABCD
известно, что \angle ABD=\angle ACD=45^{\circ}
, \angle BAC=30^{\circ}
, BC=1
. Найдите AD
.
Ответ. \sqrt{2}
.
Указание. Докажите, что точки A
, B
, C
и D
лежат на одной окружности и примените обобщённую теорему синусов (a=2R\sin\alpha)
.
Решение. Поскольку из точек B
и C
, расположенных по одну сторону от прямой AD
, отрезок AD
виден под одним и тем же углом, то точки A
, B
, C
и D
лежат на одной окружности. Пусть R
— радиус этой окружности. Тогда из треугольника ABC
находим, что
R=\frac{BC}{2\sin\angle BAC}=\frac{1}{2\sin30^{\circ}}=1,
а из треугольника ABD
—
AD=2R\sin\angle ABD=2\sin45^{\circ}=\sqrt{2}.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 7.2.24, с. 98
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 13.12, с. 103
