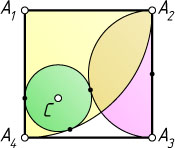
13265. Дан квадрат A_{1}A_{2}A_{3}A_{4}
со стороной 25. Окружность с центром C
касается внешним образом полуокружности с диаметром A_{2}A_{3}
, внутренним образом — расположенной внутри квадрата четверти окружности с центром A_{1}
и радиусом A_{1}A_{2}
, а также стороны A_{1}A_{4}
квадрата (см. рис.). Найдите радиус окружности.
Ответ. 9-\sqrt{6}
.
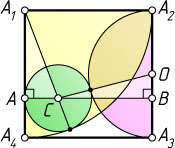
Решение. Пусть r
— радиус окружности, O
— центр полуокружности, т. е. середина стороны A_{2}A_{3}
. Через точку C
параллельно стороне A_{1}A_{2}
проведём прямую, пересекающую стороны A_{1}A_{4}
и A_{2}A_{3}
в точках A
и B
соответственно. Тогда
AB=A_{1}A_{2}=25,~CA=r,~BC=AB-AC=25-r.
Линия центров касающихся окружностей проходит через их точку касания, поэтому
CA_{1}=25-r,~CO=r+\frac{25}{2}.
По теореме Пифагора
A_{2}B=A_{1}A=\sqrt{(25-r)^{2}-r^{2}}=\sqrt{625-50r}=5\sqrt{25-2r},~r\leqslant\frac{25}{2}.
При этом
OB=OA_{3}-A_{3}B=OA_{3}-AA_{4}=\frac{25}{2}-(A_{1}A_{4}-A_{1}A)=
=\frac{25}{2}-(25-5\sqrt{25-2r})=5\sqrt{25-2r}-\frac{25}{2}.
По теореме Пифагора
BC^{2}+BO^{2}=CO^{2},
или
(25-r)^{2}+\left(5\sqrt{25-2r}-\frac{25}{2}\right)^{2}=\left(r+\frac{25}{2}\right)^{2},
5\sqrt{25-2r}=50-5r,~\sqrt{25-2r}=10-r,~r\leqslant10.
После возведения в квадрат и очевидных упрощений получаем квадратное уравнение r^{2}-18r+75=0
с корнями r=9+\sqrt{6}\gt10
, r=9-\sqrt{6}\lt10
. Условию задачи удовлетворяет только r=9-\sqrt{6}
.
Источник: Журнал «Crux Mathematicorum». — 2020, № 7, задача 4520, с. 330

