1327. Найдите периметр треугольника, один из углов которого равен \alpha
, а радиусы вписанной и описанной окружностей равны r
и R
.
Ответ. 2\left(r\ctg\frac{\alpha}{2}+2R\sin\alpha\right)
.
Указание. Примените обобщённую теорему синусов (a=2R\sin\alpha)
и теорему о равенстве отрезков касательных, проведённых к окружности из одной точки.
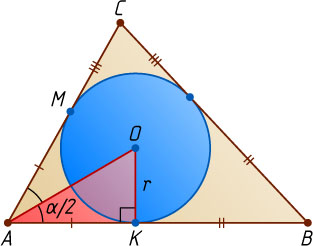
Решение. Пусть угол A
треугольника ABC
равен \alpha
, O
— центр вписанной окружности, K
— точка касания вписанной окружности со стороной AB
, M
— со стороной AC
. Тогда
BC=2R\sin\alpha,~AK=OK\ctg\frac{\alpha}{2}=r\ctg\frac{\alpha}{2}.
Поскольку AM=AK
и BK+CM=BC
, то
AB+AC+BC=2AK+2BC=2r\ctg\frac{\alpha}{2}+4R\sin\alpha.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 7.2.25, с. 98
Источник: Шарыгин И. Ф. Геометрия 7—9: Учебник для общеобразовательных учебных заведений. — М.: Дрофа, 2002. — № 31, с. 191
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 3, задача 2
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2, с. 166
