1330. Точки A
, B
и C
расположены на одной прямой. Через точку B
проходит некоторая прямая. Пусть M
— произвольная точка на этой прямой. Докажите, что расстояние между центрами окружностей, описанных около треугольников ABM
и CBM
не зависит от положения точки M
. Найдите это расстояние, если AC=a
, \angle MBC=\alpha
.
Ответ. \frac{a}{2\sin\alpha}
.
Указание. Опустите перпендикуляры из центров указанных окружностей на прямую AC
.
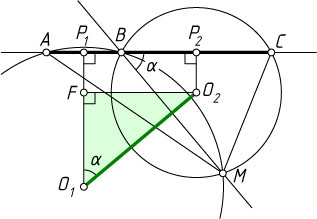
Решение. Рассмотрим случай, изображённый на рисунке. Пусть O_{1}
и O_{2}
— центры описанных окружностей треугольников ABM
и CBM
, P_{1}
и P_{2}
— проекции точек O_{1}
и O_{2}
на прямую AC
, F
— проекция точки O_{2}
на прямую P_{1}O_{1}
.
Поскольку O_{1}P_{1}
и O_{2}P_{2}
— серединные перпендикуляры к отрезкам AB
и AC
, то
P_{1}P_{2}=\frac{1}{2}AC=\frac{a}{2}.
Тогда и O_{2}F=\frac{a}{2}
, а так как
\angle FO_{1}O_{2}=\angle MBC=\alpha,
то из прямоугольного треугольника O_{1}O_{2}F
находим, что
O_{1}O_{2}=\frac{O_{2}F}{\sin\angle FO_{1}O_{2}}=\frac{a}{2\sin\alpha}.
Для остальных случаев аналогично.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 7.2.28, с. 98
