13304. Вычислите площадь общей части двух ромбов, из которых у первого диагонали равны 2 и 3, а второй получается поворотом первого на 90^{\circ}
относительно его центра.
Ответ. \frac{12}{5}
.
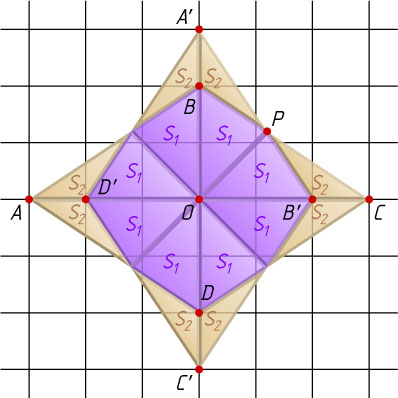
Решение. Пусть AB
— сторона ромба ABCD
с центром O
,
OA=\frac{1}{2}\cdot3=\frac{3}{2},~OB=\frac{1}{2}\cdot2=1;
при повороте относительно точки O
вершины A
и B
переходят в точки A'
и B'
, а P
— точка пересечения отрезков A'B'
и BC
. Тогда площадь S
общей части ромбов в восемь раз больше площади каждого из равных треугольников BOP
и B'OP
.
Обозначим
S_{\triangle BOP}=S_{\triangle B'OP}=S_{1},~S_{\triangle BA'P}=S_{2}.
Поскольку A'B=\frac{1}{2}
и BO=1
, то S_{2}=\frac{1}{2}S_{1}
, а так как
S_{2}+2S_{1}=S_{\triangle A'OB'}=\frac{1}{2}OA'\cdot OB'=\frac{1}{2}\cdot\frac{3}{2}\cdot1=\frac{3}{4},
то
\frac{1}{2}S_{1}+2S_{1}=\frac{3}{4},
откуда находим, что S_{1}=\frac{3}{10}
. Следовательно,
S=8S_{1}=8\cdot\frac{3}{10}=\frac{12}{5}.
Источник: Математическая олимпиада МГУ «Ломоносов». — тренировочные задачи, № 6, вариант 5, 8-9 классы
Источник: Бегунц А. В., Бородин П. А. и др. Олимпиада школьников «Ломоносов» по математике (2005—2018). — М.: МЦНМО, 2019. — с. 119
