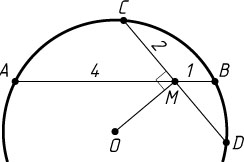
1331. В окружности с центром O
проведены хорды AB
и CD
, пересекающиеся в точке M
, причём AM=4
, MB=1
, CM=2
. Найдите угол OMC
.
Ответ. 90^{\circ}
.
Указание. Примените теорему о произведениях отрезков пересекающихся хорд.
Решение. Из равенства AM\cdot MB=CM\cdot MD
следует, что
MD=\frac{AM\cdot MB}{CM}=\frac{4\cdot1}{2}=2,
т. е. M
— середина хорды CD
. Поскольку диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде, то \angle OMC=90^{\circ}
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 7.3.8, с. 102
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.10, с. 93
