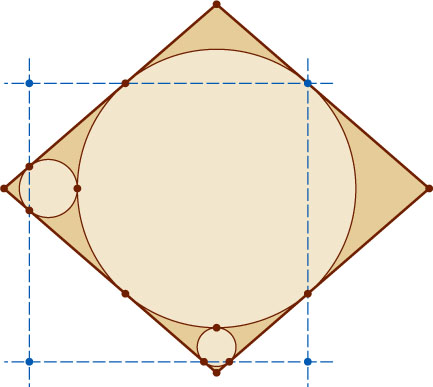
13318. Большая окружность вписана в ромб, каждая из двух меньших окружностей касается двух сторон ромба и большой окружности. Через точки касания окружностей со сторонами ромба провели четыре штриховые прямые. Докажите, что они образуют квадрат.
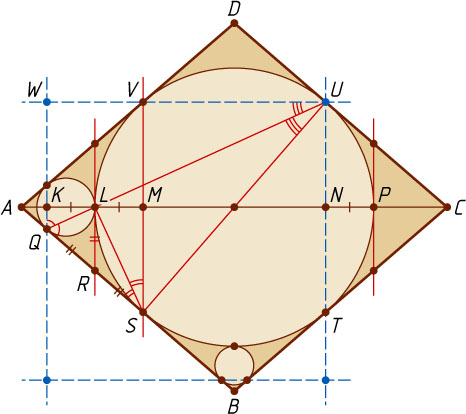
Решение. Первый способ. Полученный четырёхугольник — прямоугольник, поскольку его стороны из симметрии перпендикулярны диагоналям ромба. Осталось проверить равенство его сторон. Для этого проведём несколько дополнительных прямых, перпендикулярных диагонали AC
, и обозначим некоторые точки. Докажем, что KL=LM
.
Поскольку RQ=RL=RS
как отрезки касательных, проведённых из одной точки, то по теореме Фалеса получаем KL=LM
.
Можно по-другому: \angle KQL=\angle RQL
(эти углы измеряются половинами равных дуг), т. е. QL
— биссектриса угла KQR
. Аналогично, SL
— биссектриса угла ASM
, следовательно, точка L
равноудалена от прямых KQ
, AB
и SM
, т. е. KL=LM
.
Далее, одна из сторон полученного в условии прямоугольника равна отрезку KN
. Из симметрии LM=NP
. Тогда KN=LP
, т. е. диаметру вписанной в ромб окружности. Аналогично и другая сторона прямоугольника равна этому диаметру. Что и требовалось доказать.
Второй способ. Рассмотрим гомотетию с центром L
, переводящую маленькую окружность, вписанную в угол A
, в большую окружность. Она переводит прямую AQ
в параллельную ей касательную к большой окружности, т. е. в прямую CU
. При этом точка Q
переходит в точку U
, значит, точки Q
, L
, U
лежат на одной прямой. Далее, \angle VUL=\angle LUS
как вписанные опирающиеся на симметричные дуги, поэтому прямоугольные треугольники QUW
и QUS
равны по гипотенузе и острому углу. Следовательно, UW=US
. Аналогично, смежная с UW
сторона полученного прямоугольника равна US
. Что и требовалось доказать.
Автор: Бакаев Е. В.
Источник: Турнир городов. — 2022-2023, XLIV, осенний тур, базовый вариант, 9 октября, задача 2, 10-11 класс

