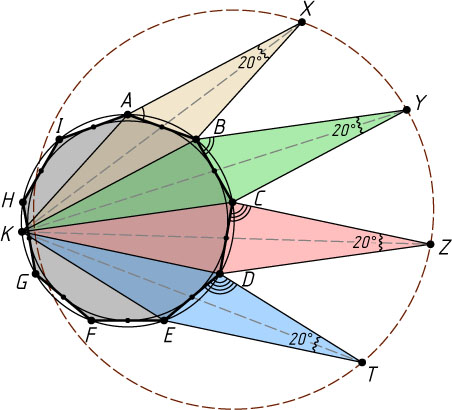
13319. На сторонах правильного девятиугольника ABCDEFGHI
во внешнюю сторону построили треугольники XAB
, YBC
, ZCD
и TDE
. Известно, что углы X
, Y
, Z
, T
этих треугольников равны 20^{\circ}
каждый, а среди углов XAB
, YBC
, ZCD
и TDE
каждый следующий на 20^{\circ}
больше предыдущего. Докажите, что точки X
, Y
, Z
, T
лежат на одной окружности.
Решение. Пусть O
— центр описанной окружности данного правильного девятиугольника. Отразив точку X
относительно середины AB
, получим точку K
, лежащую, во-первых, на этой окружности, так как
\angle AKB=\angle BXA=20^{\circ}=\frac{1}{2}\cdot40^{\circ}=\frac{1}{2}\angle AOB,
а во-вторых, — на большей дуге AC
этой окружности, так как
\angle KBA=\angle XAB=\angle YBC-20^{\circ}\lt160^{\circ}-20^{\circ}=\angle CBA,
т. е. луч BK
лежит между сторонами угла CBA
.
Поскольку
\angle KCB=\angle KCA+\angle ACB=\angle KBA+20^{\circ}=\angle XAB+20^{\circ}=\angle YBC,
то
\angle KBC=180^{\circ}-\angle BKC-\angle KCB=180^{\circ}-20^{\circ}-\angle YBC=
=160^{\circ}-\angle YBC=\angle YCB.
Значит, треугольники KCB
и YBC
равны по общей стороне BC
и двум прилежащим к ней углам, поэтому BKCY
— параллелограмм, и точка Y
симметрична точке K
относительно середины BC
. Аналогично, точки Z
и T
симметричны точке K
относительно середин CD
и DE
соответственно. Следовательно, точки X
, Y
, Z
, T
лежат на окружности, получающейся из окружности, проходящей через середины сторон девятиугольника, гомотетией с центром K
и коэффициентом 2.
Автор: Бакаев Е. В.
Источник: Турнир городов. — 2022-2023, XLIV, осенний тур, сложный вариант, 23 октября, задача 5, 10-11 класс
