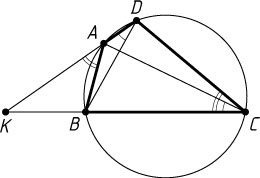
1332. Во вписанном четырёхугольнике ABCD
известны отношения AB:DC=1:2
и BD:AC=2:3
. Найдите DA:BC
.
Ответ. 1:4
.
Указание. Пусть прямые AD
и BC
пересекаются в точке K
. Тогда треугольник KAC
подобен треугольнику KBD
, а треугольник KAB
— треугольнику KCD
.
Решение. Пусть прямые AD
и BC
пересекаются в точке K
(они не могут быть параллельными, так как AB\ne CD
). Поскольку
\angle KCA=\angle BCA=\angle BDA=\angle KDB,
то треугольники KAC
и KBD
подобны по двум углам. Значит, KC:KD=AC:BD=3:2
. Пусть KC=3a
, KD=2a
. Поскольку
\angle KAB=180^{\circ}-\angle BAD=\angle KCD,
то треугольники KAB
и KCD
подобны по двум углам. Значит,
KB:KD=KA:KC=AB:CD=1:2,
поэтому
KB=\frac{1}{2}KD=a,~KA=\frac{1}{2}KC=\frac{3a}{2}.
Тогда
BC=KC-KB=2a,~AD=KD-KA=2a-\frac{3a}{2}=\frac{a}{2}.
Следовательно, AD:BC=1:4
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 7.3.10, с. 103
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 6.19, с. 47
