13337. В выпуклом четырёхугольнике ABCD
биссектрисы углов A
и C
параллельны, а биссектрисы углов B
и D
пересекаются под углом 46^{\circ}
, как изображено на рисунке. Сколько градусов составляет острый угол между биссектрисами углов A
и B
?
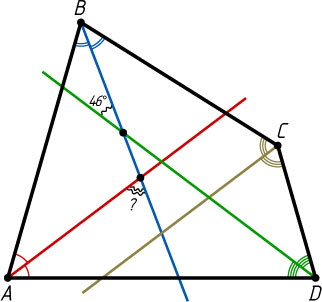
Ответ. 67^{\circ}
.
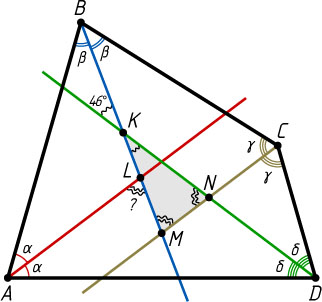
Решение. Первый способ. Пусть K
, L
, M
и N
— точки пересечения биссектрис (см. рис. 1), а углы при вершинах A
, B
, C
и D
четырёхугольника ABCD
равны 2\alpha
, 2\beta
, 2\gamma
и 2\delta
соответственно. Тогда
2\alpha+2\beta+2\gamma+2\delta=360^{\circ}~\Rightarrow~\alpha+\beta+\gamma+\delta=180^{\circ}.
Поскольку AL\parallel CM
, а ALM
— внешний угол треугольника ABL
, в треугольнике KMN
получаем
\angle KMN=\angle ALM=\alpha+\beta,
а так как
\angle KNM=\angle CND=180^{\circ}-\gamma-\delta=\alpha+\beta,
то треугольник KMN
равнобедренный. Следовательно,
\angle KMN=\frac{180^{\circ}-\angle MKN}{2}=\frac{180^{\circ}-46^{\circ}}{2}=67^{\circ}.
Второй способ. Зафиксируем угол A
и перенесём параллельно угол C
так, чтобы вершина C
оказалась на биссектрисе угла A
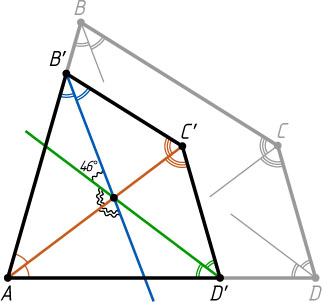
. (Или более формально, отметим на биссектрисе угла A
точку C'
и проведём из неё лучи, сонаправленные лучам CB
и CD
; пересечения этих лучей с лучами соответственно AB
и AD
обозначим через B'
и D'
, как на рис. 2.)
Стороны нового четырёхугольника AB'C'D'
соответственно параллельны сторонам исходного; значит, и углы между этими сторонами такие же. Следовательно, биссектрисы нового четырёхугольника параллельны соответствующим биссектрисам исходного, и углы между ними тоже сохранились. Но это означает, что биссектрисы углов A
и C'
совпадают, т. е. вся новая картинка симметрична относительно прямой AC'
(из равенства треугольников AB'C'
и AD'C'
по общей стороне и прилежащим к ней углам). Из симметрии следует, что другие две биссектрисы пересекаются на прямой AC'
и образуют с ней равные углы. Тогда искомый угол после удвоения будет дополнять 46^{\circ}
до развёрнутого. Следовательно, он равен
\frac{1}{2}(180^{\circ}-46^{\circ})=67^{\circ}.
Источник: Всероссийская олимпиада школьников. — 2022-2023, XLIX, муниципальный этап, задача 5, 8 класс


