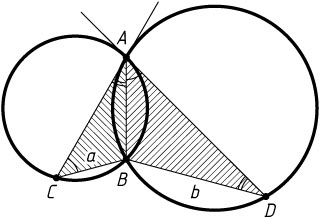
1338. Две окружности пересекаются в точках A
и B
. В каждой из этих окружностей проведены хорды AC
и AD
, причём хорда одной окружности касается другой окружности. Найдите AB
, если CB=a
, DB=b
.
Ответ. \sqrt{ab}
.
Указание. Треугольники ABC
и DBA
подобны.
Решение. Из теоремы об угле между касательной и хордой следует, что
\angle BAC=\angle BDA,~\angle BAD=\angle BCA,
поэтому треугольники ABC
и DBA
подобны по двум углам. Следовательно,
\frac{AB}{BD}=\frac{BC}{AB},
откуда находим, что
AB^{2}=BC\cdot BD=ab.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 8.2.10, с. 125
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 74
