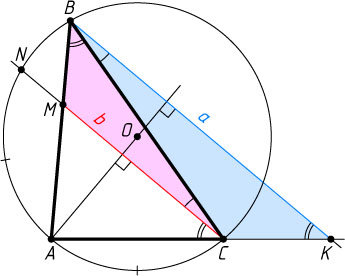
1339. В треугольнике ABC
точка O
является центром описанной окружности. Через вершину B
проведена прямая, перпендикулярная AO
, пересекающая прямую AC
в точке K
, а через вершину C
проведена прямая, также перпендикулярная AO
, пересекающая сторону AB
в точке M
. Найдите BC
, если BK=a
, CM=b
.
Ответ. \sqrt{ab}
.
Указание. Треугольники BCM
и KBC
подобны.
Решение. Из параллельности прямых KB
и CM
следует, что
\angle BCM=\angle KBC,~\angle AKB=\angle ACM.
Пусть прямая CM
вторично пересекает окружность в точке N
. Тогда
\angle ACM=\angle ACN=\frac{1}{2}\cup AN=\frac{1}{2}\cup AC=\angle ABC=\angle MBC,
поэтому треугольники BCM
и KBC
подобны. Следовательно, \frac{BC}{KB}=\frac{CM}{BC}
, откуда находим, что BC^{2}=BK\cdot CM=ab
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 8.2.11, с. 125
