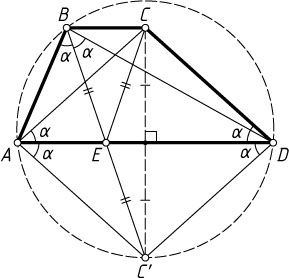
13393. На основании AD
трапеции ABCD
отмечена точка E
. Известно, что
\angle CAD=\angle ADC=\angle ABE=\angle DBE.
Докажите, что треугольник BCE
равнобедренный.
Решение. Обозначим через \alpha
угол CAD
и равные ему углы. Пусть C'
— точка, симметричная точке C
относительно прямой AD
. Тогда ACDC'
— ромб. Напишем сумму углов треугольника ADC'
:
180^{\circ}=\angle AC'D+2\alpha=\angle AC'D+\angle ABD.
Следовательно, четырёхугольник ABDC'
вписанный. Тогда
\angle ADC'=\angle ABC'=\alpha=\angle ABE.
Значит, прямая BC'
проходит через точку E
, и тогда по теореме Фалеса E
— середина отрезка BC'
(прямая DE
параллельна BC
и проходит через середину отрезка CC'
). Следовательно,
CE=C'E=BE.
Что и требовалось доказать.
Автор: Кузнецов А. С.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2020, второй тур, задача 3, 10 класс
