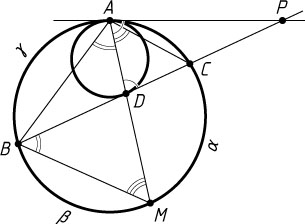
1340. Две окружности касаются друг друга внутренним образом в точке A
. Хорда BC
в большей окружности касается меньшей в точке D
. Прямая AD
вторично пересекает большую окружность в точке M
. Найдите MB
, если MA=a
, MD=b
.
Ответ. \sqrt{ab}
.
Указание. Точка M
— середина дуги BC
.
Решение. Докажем сначала, что точка M
— середина дуги BC
, не содержащей точки A
. Пусть общая касательная к данным окружностям, проведённая через точку A
, пересекает прямую BC
в точке P
(C
между B
и P
). Тогда \angle MAP=\angle ADP
как углы при основании равнобедренного треугольника APD
.
Пусть \alpha
, \beta
и \gamma
— угловые величины дуг CM
(не содержащей точки A
), BM
(не содержащей точки A
) и AB
(не содержащей точки C
) соответственно. Тогда из равенства углов MAP
и ADP
следует равенство смежных им углов, поэтому
\frac{\alpha+\gamma}{2}=\frac{\gamma+\beta}{2},
откуда получаем, что \alpha=\beta
. Значит,
\angle DBM=\angle CBM=\angle CAM=\angle BAM
и треугольники BDM
и ABM
подобны по двум углам. Следовательно,
\frac{BM}{DM}=\frac{AM}{BM},
откуда находим, что BM^{2}=AM\cdot DM=ab
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 8.2.12, с. 125
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.33, с. 114
