1341. Около окружности описана равнобедренная трапеция. Боковая сторона трапеции равна a
, отрезок, соединяющий точки касания боковых сторон с окружностью, равен b
. Найдите диаметр окружности.
Ответ. \sqrt{ab}
.
Указание. Треугольник, вершины которого — центр окружности, точка касания с боковой стороной трапеции и середина этой стороны, подобен треугольнику, вершины которого — центр окружности, точка касания с боковой стороной трапеции и середина отрезка с концами в указанных точках касания.
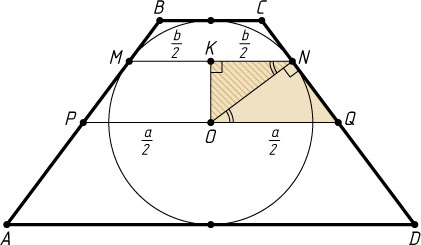
Решение. Пусть вписанная окружность касается боковой стороны AB
трапеции ABCD
в точке M
, а боковой стороны CD
— в точке N
. Центр O
этой окружности расположен на средней линии PQ
трапеции (точка Q
— середина CD
), а проекция K
точки O
на MN
— середина MN
.
По свойству описанного четырёхугольника
PQ=\frac{AD+BC}{2}=\frac{AB+CD}{2}=\frac{a+a}{2}=a.
Тогда OQ=\frac{1}{2}a
.
Из подобия треугольников OKN
и QNO
следует, что
\frac{KN}{ON}=\frac{ON}{OQ},
откуда находим, что
ON^{2}=OQ\cdot KN=\frac{1}{2}a\cdot\frac{1}{2}b=\frac{1}{4}ab,~ON=\frac{1}{2}\sqrt{ab}.
Поскольку ON
— радиус вписанной окружности, диаметр окружности равен \sqrt{ab}
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 8.2.16, с. 125
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.16, с. 112
