1342. Биссектриса CM
угла треугольника ABC
делит сторону AB
на отрезки AM=a
и BM=b
(a\gt b
). Касательная к описанной окружности треугольника ABC
, проходящая через точку C
, пересекает прямую AB
в точке D
. Найдите CD
.
Ответ. \frac{ab}{a-b}
.
Указание. Треугольники DAC
и DCB
подобны.
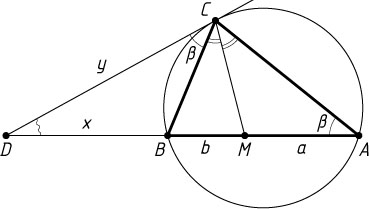
Решение. Первый способ. Пусть CM
— биссектриса треугольника ABC
, AM=a
, BM=b
(рис. 1). По свойству биссектрисы треугольника
\frac{AC}{CB}=\frac{AM}{MB}=\frac{a}{b}.
Положим BD=x
, CD=y
. Из равенства углов BAC
и BCD
следует подобие треугольников DAC
и DCB
, значит,
\frac{BD}{CD}=\frac{CD}{AD}=\frac{CB}{AC}=\frac{b}{a},~\mbox{или}~\frac{x}{y}=\frac{y}{x+a+b}=\frac{b}{a}.
Из этой системы уравнений находим, что y=\frac{ab}{a-b}
.
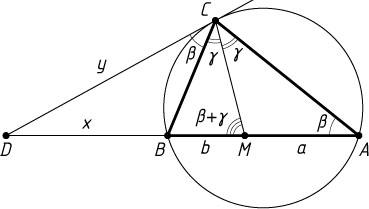
Второй способ. Пусть CM
— биссектриса треугольника ABC
, AM=a
, BM=b
(рис. 2). Обозначим
\angle ACM=\angle BCM=\gamma,~\angle BCD=\angle CAD=\beta.
По теореме о внешнем угле треугольника
\angle CMD=\angle ACM+\angle MAC=\gamma+\beta,
а так как
\angle DCM=\angle BCM+\angle BCD=\gamma+\beta,
то треугольник DCM
— равнобедренный, DM=DC
.
Положим BD=x
, CD=y
. Тогда
y=CD=DM=BD+BM=x+b,
а по теореме о касательной и секущей
y^{2}=CD^{2}=BD\cdot AD=x(x+a+b).
Из системы
\syst{y=x+b\\y^{2}=x(x+a+b)\\}
находим, что y=\frac{ab}{a-b}
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 8.2.18, с. 126
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 12.44, с. 119
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 12.42.1, с. 129
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 931, с. 114

