13441. Существует ли четырёхугольник, отличный от прямоугольника, у которого есть три равных угла?
Ответ. Существует.
Решение. Приведём два примера таких четырёхугольников.
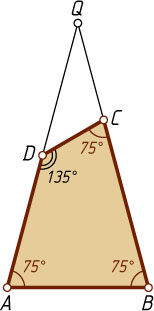
1. Выпуклый. Рассмотрим равнобедренный треугольник ABQ
, в котором \angle A=\angle B=75^{\circ}
(рис. 1). На стороне AQ
отметим произвольную точку D
и построим угол ADC
, равный 135^{\circ}
. Тогда \angle BCD=75^{\circ}
. Тогда четырёхугольник ABCD
искомый.
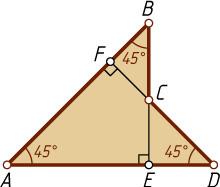
2. Невыпуклый. Рассмотрим два прямоугольных равнобедренных треугольника ABE
и ADF
(не обязательно равных). Наложим их друг на друга так, как показано на рис. 2. Пусть BE
и DF
пересекаются в точке C
, тогда четырёхугольник ABCD
искомый.
Существуют и другие примеры.
Источник: Московская математическая регата. — 2022, задача 1.2, 9 класс

