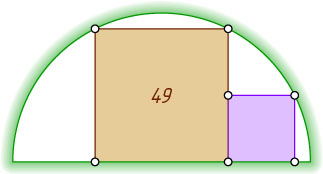
13443. В полукруг вписан квадрат площади 49, к которому примыкает ещё один квадрат, одна из вершин которого лежит на полуокружности (см. рисунок). Найдите площадь второго квадрата.
Ответ. 12,25.
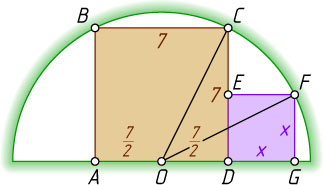
Решение. Обозначим вершины квадратов так, как показано на рис. 1. Из условия следует, что сторона большего квадрата равна 7. В силу симметрии, центр O
данного полукруга — середина стороны AD
. Далее можно рассуждать по-разному.
Первый способ. Обозначим через x
сторону второго квадрата. Проведём радиусы OC
и OF
. Из прямоугольного треугольника OCD
находим, что
OC^{2}=7^{2}+\left(\frac{7}{2}\right)^{2},
а из прямоугольного треугольника OFG
—
OF^{2}=\left(\frac{7}{2}+x\right)^{2}+x^{2}.
Учитывая, что OF=OC
, получим
7^{2}+\left(\frac{7}{2}\right)^{2}=\left(\frac{7}{2}+x\right)^{2}+x^{2},~\mbox{или}~2x^{2}+7x-49=0.
Условию задачи удовлетворяет только положительный корень x=\frac{7}{2}
этого уравнения. Следовательно, искомая площадь равна \frac{49}{4}=12{,}25
.
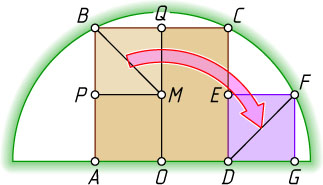
Второй способ. Пусть M
— центр квадрата ABCD
, а P
и Q
— середины сторон AB
и BC
(см. рис. 2). Рассмотрим поворот с центром O
на 90^{\circ}
по часовой стрелке. При этом повороте угол PMQ
и его биссектриса, на которой лежит точка B
, перейдут в угол EDG
и его биссектрису, на которой лежит точка F
, а так как окружность при указанном повороте переходит в себя, то точка B
переходит в точку F
. Таким образом, квадрат PBQM
переходит в квадрат DEFG
. Следовательно, площадь DEFG
в четыре раза меньше площади ABCD
, т. е. она равна \frac{49}{4}
.
Примечание. В первом способе можно обойтись без уравнения. Заметим, что если x\lt\frac{7}{2}
, то оба катета треугольника OCD
больше соответствующих катетов треугольника FOG
, а если x\gt\frac{7}{2}
, то наоборот. Поэтому в обоих случаях их гипотенузы не могут быть равны. Значит, x=\frac{7}{2}
.
Источник: Московская математическая регата. — 2022, задача 3.2, 9 класс


