13447. Два правильных шестиугольника с отношением сторон 1:2
расположены так, как показано на рисунке. Найдите AN
, если CL=6
.
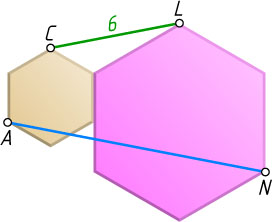
Ответ. 12.
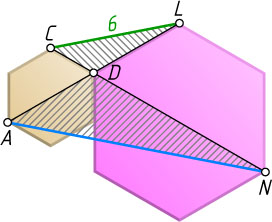
Решение. Первый способ. Через общую вершину D
двух шестиугольников и проведём их большие диагонали AD
и DN
(рис. 1). Они образуют со сторонами, сходящимися в вершине D
, углы 60^{\circ}
, поэтому
\angle ADN=\angle ADE+\angle NDE=60^{\circ}+60^{\circ}=120^{\circ}=\angle CDL.
Кроме того, в любом правильном шестиугольнике большая диагональ в два раза больше стороны, значит, треугольник ADN
подобен треугольнику CDL
с коэффициентом k=2
. Следовательно,
AN=2CL=12.
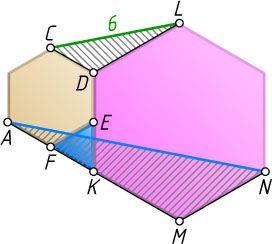
Второй способ. Введём обозначения так, как показано на рис. 2, где K
— точка пересечения лучей AF
и DE
. Угол правильного шестиугольника равен 120^{\circ}
, поэтому треугольник EKF
равносторонний. Кроме того, точки F
и K
лежат на отрезке AM
, причём
AM=AF+FK+KM=AF+AF+2AF=4AF=2KM.
Треугольник AMN
подобен треугольнику LDC
с коэффициентом 2, так как
AM=2KM=2LD,~MN=2DC,~\angle AMN=\angle LDC=120^{\circ}.
Следовательно,
AN=2CL=12.
Источник: Московская математическая регата. — 2023, задача 2.2, 10 класс


