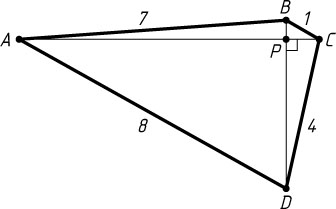
1345. Три стороны четырёхугольника в порядке обхода равны 7, 1 и 4. Найдите четвёртую сторону этого четырёхугольника, если известно, что его диагонали перпендикулярны.
Ответ. 8.
Указание. Если диагонали четырёхугольника перпендикулярны, то суммы квадратов его противоположных сторон равны.
Решение. Пусть диагонали AC
и BD
четырёхугольника ABCD
перпендикулярны и пересекаются в точке P
; AB=7
, BC=1
, CD=4
. По теореме Пифагора
AB^{2}-AP^{2}=BC^{2}-CP^{2},~\mbox{или}~AB^{2}-BC^{2}=AP^{2}-CP^{2}.
Аналогично докажем, что
AD^{2}-CD^{2}=AP^{2}-CP^{2}.
Следовательно,
AB^{2}-BC^{2}=AD^{2}-CD^{2},~\mbox{или}~AB^{2}+CD^{2}=BC^{2}+AD^{2}.
Отсюда находим, что
AD^{2}=AB^{2}+CD^{2}-BC^{2}=49+16-1=64,~AD=8.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 8.4.4, с. 136
