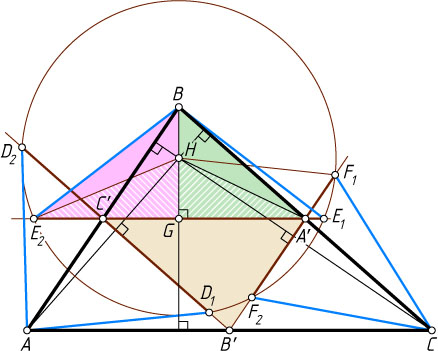
13472. Точка H
— ортоцентр треугольника ABC
, точки A'
, B'
, C'
— середины сторон BC
, CA
, AB
соответственно. Окружность с центром H
пересекает прямую B'C'
в точках D_{1}
и D_{2}
, прямую C'A'
— в точках E_{1}
и E_{2}
, прямую A'B'
— в точках F_{1}
и F_{2}
. Докажите, что
AD_{1}=AD_{2}=BE_{1}=BE_{2}=CF_{1}=CF_{2}.
Решение. Пусть точки пересечения окружности с прямыми B'C'
, C'A'
, A'B'
расположены так, как показано на рисунке. Поскольку C'B'\parallel BC
и AH\perp BC
, то AH\perp D_{1}D_{2}
, поэтому прямая AH
— серединный перпендикуляр к хорде D_{1}D_{2}
. Значит, AD_{1}=AD_{2}
. Аналогично, BE_{1}=BE_{2}
и CF_{1}=CF_{2}
. Для доказательства утверждения задачи осталось доказать, что, например, BE_{2}=CF_{1}
.
Пусть перпендикулярные прямые BH
и A'C'
пересекаются в точке G
. Тогда по теореме Пифагора
E_{2}B^{2}=BG^{2}+E_{2}G^{2}=(A'B^{2}-A'G^{2})+(E_{2}H^{2}-GH^{2})=
=A'B^{2}+E_{2}H^{2}-(A'G^{2}+GH^{2})=A'B^{2}+E_{2}H^{2}-A'H^{2}.
Аналогично,
F_{1}C^{2}=A'C^{2}+F_{1}H^{2}-A'H^{2},
а так как A'B=A'C
и E_{2}H=F_{1}H
как радиусы одной окружности, то E_{2}B=F_{1}C
. Отсюда следует утверждение задачи.
Источник: Журнал «Crux Mathematicorum». — 1990, № 6, задача 268
Источник: Британская математическая олимпиада. — 1981
