1348. Пусть в выпуклом четырёхугольнике ABCD
нет параллельных сторон. Обозначим через E
и F
точки пересечения прямых AB
и DC
, BC
и AD
соответственно (точка A
лежит на отрезке BE
, а точка C
— на отрезке BF
). Докажите, что четырёхугольник ABCD
является описанным тогда и только тогда, когда EA+AF=EC+CF
.
Указание. Докажите, что биссектрисы углов BAD
, BCD
и BEC
пересекаются в одной точке.
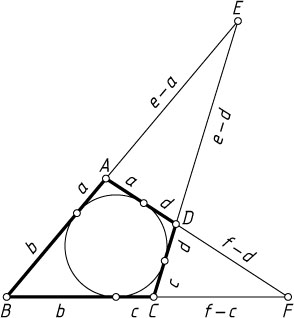
Решение. Необходимость. Дано: ABCD
— описанный четырёхугольник (рис. 1). Пусть касательные к вписанной окружности из точек A
, B
, C
, D
, E
и F
равны соответственно a
, b
, c
, d
, e
и f
. Тогда
EA=e-a,~AF=a+f,~EC=e+c,~CF=f-c.
Значит,
EA+AF=(e-a)+(a+f)=e+f,~EC+CF=(e+c)+(f-c)=e+f.
Следовательно, EA+AF=EC+CF
.
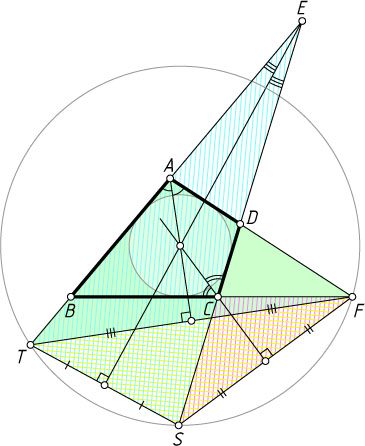
Достаточность. Пусть выполняется равенство EA+AF=EC+CF
. Докажем, что биссектрисы углов BAD
, BCD
и BEC
пересекаются в одной точке (рис. 2). Отсюда будет следовать, что ABCD
— описанный четырёхугольник. (Точка пересечения этих биссектрис будет равноудалена от AB
и AD
, BC
и CD
, а также от AB
и CD
.)
Возьмём на продолжении отрезка EA
за точку A
такую точку T
, чтобы AT=AF
, а на продолжении отрезка EC
за точку C
— такую точку S
, чтобы CS=CF
. Поскольку ET=EA+AF
, а ES=EC+CF
, то из условия следует, что ET=ES
.
Рассмотрим треугольник TFS
. Серединный перпендикуляр к стороне TS
этого треугольника является биссектрисой угла TES
(или угла BEC
). Это следует из равнобедренности треугольника TES
. Аналогично докажем, что серединный перпендикуляр к стороне TF
есть биссектриса угла TAF
(или угла BAD
), а серединный перпендикуляр к стороне SF
— биссектриса угла CSF
(или угла BCD
). Следовательно, указанные биссектрисы пересекаются в одной точке — центре описанной окружности треугольника TFS
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — с. 143
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 6.9, с. 152

