13509. Две перпендикулярные хорды разбивают круг радиуса R
на четыре криволинейных треугольника. В каждый из них вписаны окружности радиусов r_{1}
, r_{2}
, r_{3}
и r_{4}
. Докажите, что
r_{1}+r_{2}+r_{3}+r_{4}\leqslant4(\sqrt{2}-1)R.
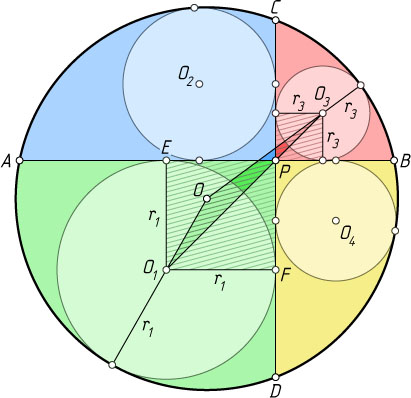
Решение. Пусть перпендикулярные хорды AB
и CD
окружности с центром O
пересекаются в точке P
, окружности с центрами O_{1}
и O_{3}
радиусов r_{1}
и r_{3}
вписаны в криволинейные треугольники APD
и BPC
соответственно. Пусть также окружность с центром O_{1}
касается AP
и DP
в точках E
и F
соответственно. Тогда
OO_{1}=R-r_{1},~OO_{3}=R-r_{3},
а так как O_{1}EOF
— квадрат, то O_{1}P=r_{1}\sqrt{2}
. Аналогично, O_{3}P=r_{3}\sqrt{2}
. Точка P
лежит на отрезке O_{1}O_{3}
, поэтому
O_{1}O_{3}=O_{1}P+O_{3}P=(r_{1}+r_{3})\sqrt{2}.
Из неравенства треугольника следует, что
O_{1}O_{3}\leqslant OO_{1}+OO_{3},~\mbox{или}~(r_{1}+r_{3})\sqrt{2}\leqslant R-r_{1}+R-r_{3},
откуда получаем, что
r_{1}+r_{3}\leqslant\frac{2R}{\sqrt{2}+1}=2R(\sqrt{2}-1).
Аналогично, r_{2}+r_{4}\leqslant2R(\sqrt{2}-1)
. Сложив эти два неравенства, получим требуемое.
Неравенство обращается в равенство, если хорды пересекаются в центре окружности.
Источник: Журнал «Crux Mathematicorum». — 1992, № 3, задача 1627 (79), с. 96
