13523. Дан неравнобедренный треугольник ABC
единичной площади. На стороне AC
отмечены точки C_{1}
и C_{2}
, а на стороне AB
— точки B_{1}
и B_{2}
, причём AC_{1}=C_{1}C_{2}=C_{2}C
и AB_{1}=B_{1}B_{2}=B_{2}B
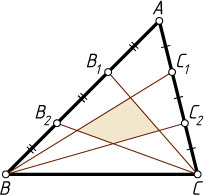
. Найдите площадь четырёхугольника, образованного пересечениями прямых BC_{1}
, BC_{2}
, CB_{1}
и BC_{2}
(см. рисунок).
Ответ. \frac{9}{70}
.
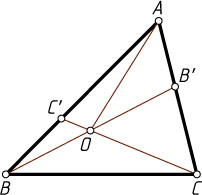
Решение. Лемма. Если точки B'
и C'
лежат на сторонах соответственно AC
и AB
треугольника ABC
, а отрезки BB'
и CC'
пересекаются в точке O
, то
\frac{BO}{OB'}=\frac{BC'}{C'A}\left(\frac{AB'}{B'C}+1\right).
Доказательство.
\frac{BO}{OB'}=\frac{S_{\triangle ABO}}{S_{\triangle AB'O}}=\frac{S_{\triangle CBO}}{S_{\triangle CB'O}}=\frac{S_{\triangle ABO}+S_{\triangle CBO}}{S_{\triangle AC'O}}=
=\frac{S_{\triangle CBO}}{S_{\triangle ACO}}\left(\frac{S_{\triangle ABO}}{S_{\triangle CBO}}+1\right)=\frac{BC'}{C'A}\left(\frac{AB'}{B'C}+1\right).
Лемма доказана.
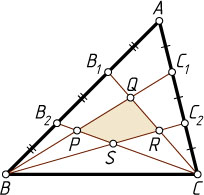
Рассмотрим теперь четырёхугольник PQRS
, о котором говорится в условии задачи. По лемме
\frac{BP}{PC_{1}}=\frac{1}{2}\left(\frac{1}{2}+1\right)=\frac{3}{4},~\frac{BQ}{QC_{1}}=2\left(\frac{1}{2}+1\right)=3,
поэтому
BP=\frac{3}{7}BC_{1},~QC_{1}=\frac{1}{4}BC_{1},
PQ=\left(1-\frac{3}{7}-\frac{1}{4}\right)BC_{1}=\frac{9}{28}BC_{1}.
Значит, BP:PQ:QC_{1}=12:9:7
.
Аналогично,
\frac{BS}{SC_{2}}=\frac{1}{2}(2+1)=\frac{3}{2},~\frac{BR}{RC_{2}}=2(2+1)=6,
поэтому
BS=\frac{3}{5}BC_{2},~RC_{2}=\frac{1}{7}BC_{2},
RS=\left(1-\frac{3}{5}-\frac{1}{7}\right)BC_{2}=\frac{9}{35}BC_{2}.
Значит, BS:SR:RC_{2}=21:9:5
. Тогда
S_{\triangle BPS}=\frac{BP}{BQ}\cdot\frac{BS}{BR}S_{\triangle BQR}=\frac{12}{21}\cdot\frac{21}{30}S_{\triangle BQR}=\frac{2}{5}S_{\triangle BQR},
Следовательно,
S_{PQRS}=\frac{3}{5}S_{\triangle BQR}=\frac{3}{5}\cdot\frac{BQ}{BC_{1}}\cdot\frac{BR}{BC_{2}}S_{\triangle BC_{1}C_{2}}=\frac{3}{5}\cdot\frac{3}{4}\cdot\frac{6}{7}\cdot\frac{1}{3}=\frac{9}{70}.
Источник: Журнал «Crux Mathematicorum». — 1993, № 1, задача 1708 (13), с. 20


