1353. На прямой расположены три точки A
, B
и C
, причём AB=BC=3
. Три окружности радиуса R
имеют центры в точках A
, B
и C
. Найдите радиус четвёртой окружности, касающейся всех трёх данных, если а) R=1
; б) R=2
; в) R=5
.
Ответ. а) \frac{9}{4}
и \frac{9}{2}
; б) \frac{9}{8}
; в) \frac{9}{20}
и \frac{9}{10}
.
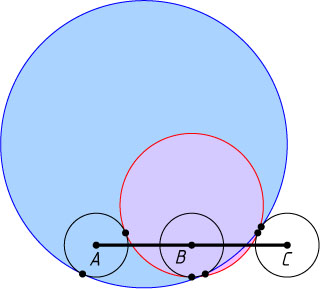
Указание. Обозначим через x
радиус искомой окружности, O
— её центр. Расстояния до центров данных окружностей до точки O
может быть равно либо x+R
(внешнее касание), либо |x-R|
(внутреннее касание). Все три отрезка равными быть не могут. Рассмотрите все возможные случаи.
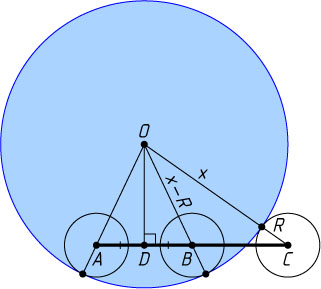
Решение. Решим задачу в общем виде. Обозначим через x
радиус искомой окружности, O
— её центр. Расстояния от центров данных окружностей до точки O
могут быть равны либо x+R
(внешнее касание), либо |x-R|
(внутреннее касание). Все три отрезка равными быть не могут. Значит, возможны два случая.
1) OA=OC=x+R
, OB=|x-R|
. По теореме Пифагора из прямоугольного треугольника OAB
(рис. 1) находим, что
(x+R)^{2}-(x-R)^{2}=9.
Откуда x=\frac{9}{4R}
.
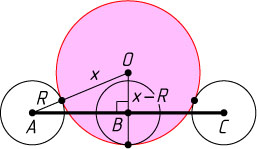
2) OA=OB=|x-R|
, OC=x+R
. Пусть D
— середина AB
(рис. 2). Тогда
OD^{2}=OC^{2}-DC^{2}=(x+R)^{2}-\frac{81}{4},
значит,
(x-R)^{2}-\frac{9}{4}=(x+R)^{2}-\frac{81}{4},~x=\frac{9}{2R}.
При этом должны выполняться условия:
(x+R)+|x-R|\geqslant6,~(x+R)-|x-R|\leqslant3.
Решая эти неравенства при x=\frac{9}{2R}
, получим, что R\leqslant\frac{3}{2}
или R\geqslant3
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 8.6.10, с. 156
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — N№ 9.34, 9.35, с. 70




