1355. В треугольнике ABC
сторона BC
равна 4, а медиана, проведённая к этой стороне, равна 3. Найдите длину общей хорды двух окружностей, каждая из которых проходит через точку A
и касается BC
, причём одна касается BC
в точке B
, а вторая — в точке C
.
Ответ. \frac{5}{3}
.
Указание. Докажите, что продолжение общей хорды указанных окружностей проходит через середину BC
.
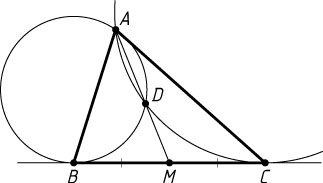
Решение. Пусть D
— вторая точка пересечения указанных окружностей, а прямая AD
пересекает BC
в точке M
. Тогда по теореме о касательной и секущей
MB^{2}=MA\cdot MD=MC^{2},
поэтому MB=MC
, т. е. AM
— медиана треугольника ABC
, AM=3
. Из уравнения
MA(MA-AD)=MB^{2},~\mbox{или}~3(3-AD)=4
находим, что AD=\frac{5}{3}
.
