13559. Дан равнобедренный треугольник ABC
с основанием BC
. Касательные к его описанной окружности, проведённые в точках A
и C
, пересекаются в точке D
. Докажите, что \angle DBC\leqslant30^{\circ}
.
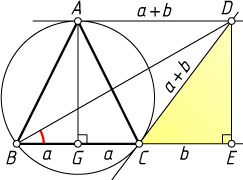
Решение. Первый способ. Пусть G
— середина BC
, а DE
— перпендикуляр к прямой BC
(рис. 1). Обозначим BG=CG=a
, CE=b
. Тогда AGED
— прямоугольник, в котором AD=GE=a+b
, а также DC=DA=GE=a+b
. По теореме Пифагора из прямоугольного треугольника CED
получаем, что
DE^{2}=DC^{2}-CE^{2}=(a+b)^{2}-b^{2}=a^{2}+2ab.
Тогда
\angle DBC\leqslant30^{\circ}~\Leftrightarrow~\angle DBE\leqslant30^{\circ}~\Leftrightarrow~\tg\angle DBE\leqslant\frac{1}{\sqrt{3}}~\Leftrightarrow~\frac{DE}{BE}\leqslant\frac{1}{\sqrt{3}}\leqslant
\leqslant3DE^{2}\leqslant BE^{2}~\Leftrightarrow~3(a^{2}+2ab)\leqslant(2a+b)^{2}~\Leftrightarrow~0\leqslant(a-b)^{2}.
Из последнего очевидного неравенства следует утверждение задачи.
Заметим что равенство достигается тогда и только тогда, когда треугольник ABC
равносторонний.
Второй способ. Лемма. Если в треугольнике XYZ
известно, что XY=2XZ
, то \angle XYZ\leqslant30^{\circ}
.
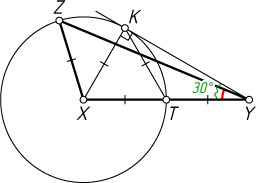
Доказательство. (Это утверждение можно легко доказать с помощью теоремы синусов, но мы изложим изящное геометрическое доказательство без применения тригонометрии.) Пусть T
— середина стороны XY
, а YK
— касательная к окружности с центром X
и радиусом XK=XZ
(рис. 2). Тогда XK=XT=TK
(так как медиана KT
прямоугольного треугольника XKY
равна половине гипотенузы XY
), а треугольник XTK
равносторонний. Следовательно,
\angle XYZ\leqslant\angle XYK=30^{\circ}.
Лемма доказана.
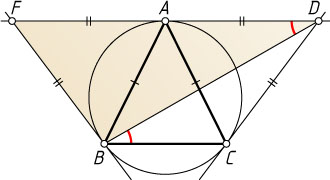
Перейдём к нашей задаче. Пусть F
— точка, симметричная точке D
относительно A
(рис. 3). Тогда FB=FA=AD
. Следовательно, применив лемму к треугольнику BDF
, получим, что
\angle DBC=\angle BDF\leqslant30^{\circ}.
Что и требовалось доказать.
Источник: Журнал «Crux Mathematicorum». — 1995, № 5, задача 1961 (1994, с. 193), с. 175


