1356. Острый угол равнобедренной трапеции равен 75^{\circ}
. Прямые, проходящие через концы одного из оснований трапеции параллельно противоположным боковым сторонам, пересекаются на окружности, описанной около трапеции. Найдите отношение оснований трапеции.
Ответ. \sqrt{3}
.
Указание. Докажите, что указанные прямые не могут проходить через концы большего основания трапеции. Примените обобщённую теорему синусов (a=2R\sin\alpha
).
Решение. Пусть указанные прямые проходят через концы A
и D
большего основания AD
данной трапеции ABCD
и пересекаются в точке M
, расположенной на описанной окружности трапеции ABCD
. Поскольку AM\parallel CD
, то \angle MDA=\angle BAD=75^{\circ}
. Аналогично \angle MAD=75^{\circ}
. Тогда угол AMD
треугольника AMD
равен
180^{\circ}-2\cdot75^{\circ}=30^{\circ},
а так как точки M
и B
лежат по разные стороны от хорды AD
, то
\angle ABD=180^{\circ}-\angle AMD=150^{\circ},
что невозможно, так как угол ABD
есть часть угла ABC
, равного 105^{\circ}
.
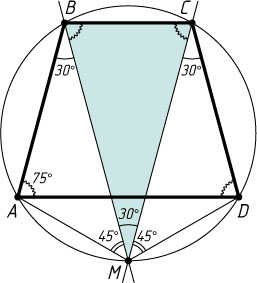
Пусть теперь указанные прямые проходят через концы B
и C
меньшего основания данной трапеции и пересекаются в точке M
, расположенной на описанной окружности этой трапеции. Тогда
\angle BMC=180^{\circ}-(\angle MBC+\angle MCB)=180^{\circ}-(\angle ADC+\angle BAD)=
=180^{\circ}-150^{\circ}=30^{\circ}.
Поскольку точки M
и A
лежат по одну сторону от хорды BD
, То
\angle BMD=\angle BAD=75^{\circ}.
Значит,
\angle AMB=\angle CMD=\angle BMD-\angle BMC=75^{\circ}-30^{\circ}=45^{\circ},
\angle AMD=\angle AMB+\angle BMC+\angle CMD=30^{\circ}+45^{\circ}+45^{\circ}=120^{\circ}.
Обозначим через R
радиус описанной окружности данной трапеции. Тогда
BC=2R\sin\angle BMC=2R\sin30^{\circ}=R,
AD=2R\sin\angle AMD=2R\sin120^{\circ}=R\sqrt{3}.
Следовательно, \frac{AD}{BC}=\sqrt{3}
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 53, с. 163
