13565. На сторонах треугольника ABC
вне треугольника построены три подобных треугольника DBC
, ECA
и FAB
. При этом \angle DBC=\angle ECA=\angle FAB
и \angle DCB=\angle EAC=\angle FBA
. Отрезки BE
и CF
пересекаются в точке P
, отрезки CF
и AD
— в точке Q
, а отрезки AD
и BE
— в точке R
. Докажите, что
\frac{QR}{AD}=\frac{RP}{BE}=\frac{PQ}{CF}.
Решение. Если прямые AD
, BE
и CF
пересекаются в одной точке, утверждение очевидно. Предположим, что точки P
, Q
и R
попарно различны.
Достроим треугольник AEB
до параллелограмма AEBG
. Обозначим BC=a
, AC=b
, AB=c
. Отношение соответствующих сторон подобных треугольников BCD
, CAE
и ABF
равно a:b:c
, поэтому стороны треугольника BCD
равны ax
, ay
, az
, стороны треугольника CAE
равны bx
, by
, bz
, стороны треугольника ABF
равны cx
, cy
, cz
(как показано на рисунке).
Поскольку AEBG
— параллелограмм,
GB=AY=by,~\frac{BF}{BG}=\frac{c}{b}=\frac{AB}{AC},
а так как \angle GBA=\angle EAB
и \angle EAC=\angle FBA
, то \angle GBF=\angle CAB
. Значит, треугольники BFG
и ABC
подобны, поэтому GF=ay=DC
. Кроме того,
\angle GFC+\angle DCF=(\angle GFB+\angle BFC)+(\angle DCB+\angle BCF)=
=\angle GFB+(\angle BFC+\angle BCF)+\angle DCB=\angle ABC+(180^{\circ}-\angle FBC)+\angle FBA=
=\angle ABC+180^{\circ}-(\angle FBA+\angle ABC)+\angle FBA=180^{\circ}.
Таким образом GF\parallel DC
, а так как GF=DC
, то FGDC
— тоже параллелограмм. Тогда GD=FC
и GD\parallel FC
. Из всего этого получаем, что треугольники PQR
и GDA
подобны. Тогда
\frac{QR}{DA}=\frac{RP}{AG}=\frac{PQ}{GD},
а так как AG=BE
и GD=FC
, то
\frac{QR}{AD}=\frac{RP}{BE}=\frac{PQ}{CF}.
Что и требовалось доказать.
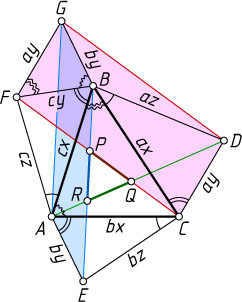
Источник: Журнал «Crux Mathematicorum». — 1995, № 10, задача 2001 (19), с. 345
Источник: Австрийско-польские математические олимпиады. — 1992
