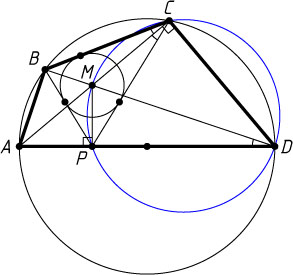
1359. Сторона AD
вписанного четырёхугольника ABCD
является диаметром описанной окружности, M
— точка пересечения диагоналей, P
— проекция M
на AD
. Докажите, что M
— центр окружности, вписанной в треугольник BCP
.
Указание. Точки P
, M
, C
и D
лежат на одной окружности.
Решение. Поскольку AD
— диаметр окружности, то \angle ACD=90^{\circ}
. Поэтому отрезок DM
виден из точек C
и P
под прямым углом. Значит, точки C
и P
лежат на окружности с диаметром DM
. Следовательно,
\angle MCP=\angle MDP=\angle BDA=\angle BCA=\angle BCM,
т. е. CA
— биссектриса угла BCP
треугольника BCP
.
Аналогично докажем, что BM
— биссектриса угла CBP
треугольника BCP
.
Источник: Шарыгин И. Ф. Геометрия — 8. Теория и задачи: Экспериментальное учебное пособие для 8 кл. — М.: РОСТ, МИРОС, 1996. — № 64, с. 164
